ecuații matematice și inegalități cu modul

ecuațiile modulului și inegalitățile

Modulul unui număr real - este valoarea absolută a acestui număr. Pur și simplu pune, modulul de captare a fi scăzut de la numărul de semnul său. notat | o |. De exemplu, | 6 | = 6, | -3 | = 3, | -10,45 | = 10,45. Definiție Modulului Modulul Proprietăți

1) Modulele sunt numere opuse | A | = | -a |. 2) numărul modulului este egală cu pătratul pătratul acestui număr | o | 2 = a 2 3) Rădăcina pătrată a unui pătrat a unui modul al acestui număr √ (a 2) = a 2. 4) Numărul modulului este un număr nenegativ | o | ≥ 0. 5) un factor constant pozitiv poate fi luat în afara mărcii modulului | Ca | = c | a |, c> 0. 6) În cazul în care | o | = | b |. apoi a = ± b. 7) Modul de produs a două (sau mai multe) numere egale cu produsul valorilor lor absolute | o # 8729; b | = | o | # 8729; | b | .

Sensul geometric al modulului Numărul modulului - distanța de la zero la un număr dat. De exemplu, | -5 | = 5. Cu alte cuvinte, distanța de la punctul zero la -5 la 5. ia în considerare cea mai simplă ecuație | x | = 3. Se poate vedea că pe linia numărul, există două puncte a căror distanță de la zero este egal cu trei. Aceasta punctele 3 și -3. Deci, ecuația | x | = 3, există două soluții: x = 3 și x = -3. Semnificația geometrică a valorilor modulului de diferență - este distanța dintre ele. De exemplu, sensul geometric al frazei | x - a | - lungimea axei de coordonate a punctului segment care unește cu abscisă x și a. Exemplul 1: rezolva ecuația: | x - 3 | = 4. Soluție. Această ecuație poate fi citită ca distanța dintre punctul x la punctul 3 este 4. Metoda grafică poate determina că ecuația are două soluții: 1 și 7. A: -1; Exemplul 7. 2. Solve inegalitatea: | x + 7 | <4. Решение. Можно прочитать как: расстояние от точки х до точки –7 меньше четырёх. Ответ: (-11; -3). Пример 3. Решить неравенство: |10 — x | ≥ 7. Решение. Расстояние от точки 10 до точки х больше или равно семи.





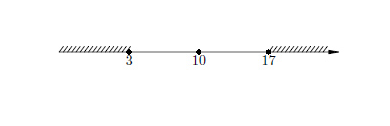
Răspuns: (-∞; 3] υ [17, + ∞). Notă. Traducerea problemă algebrică pe limba geometrică de multe ori evită greoaie. Exemplul 4. Rezolvați ecuația. | x - 1 | + | x - 2 | = 1. Soluție. Vom proceda după cum urmează: pornind de la modulul de interpretare geometrică, în partea stângă a ecuației reprezintă suma distanțelor de la un punct cu abscisa x la două puncte fixe cu abscise 1 și 2. Apoi, este evident că toate punctele cu abscisă în intervalul [1; 2] au proprietatea necesare, iar punctele sunt situate în afara acestui segment - nu. Prin urmare, răspunsul: soluția stabilită este intervalul [1; 2]. Răspuns: [1; 2]. Exemplul 5 rezolva ecuația: | x - 1 | - | x - 2 | = 1. Soluție. În mod similar, constatăm că diferența dintre distanțele la punctele 1 și 2 abscise egal cu unitatea numai pentru punctele de pe axa de coordonate a 2. Apoi răspunsul corect - cu raze [2; + ∞). Răspuns: [2; + ∞). Exemplul 6 Rezolva inegalitatea | x + 1 | + | x - 1 |> 2. Soluție. Să se reprezinte pe coordonata punctului axa, suma a cărei distanțe de puncte la -1 și 1 este exact egală cu 2. Acesta este toate punctele din intervalul [-1; 1]. Este evident că pentru toate numerele în afara acestui interval de suma distanțelor va fi mai mare de două, în cazul în care răspunsul: (-∞; -1) (1 + ∞). Răspuns: (-∞; -1) (1 + ∞). Notă. soluții generalizate ale ecuațiile de mai sus sunt următoarele tranziții sunt echivalente:

| X - o | + | X - b | = B - a, b ≥ a, a ≤ x ≤ b | x - a | - | x - b | = B - a, b ≥ a, x ≥ b