Analiza de regresie - metoda statistică de investigare dependența variabilei aleatoare de

Regresia statistică Studiul de modelare analiză este utilizată pentru a evalua relația dintre variabile. Această metodă matematică include o multitudine de alte metode pentru modelarea și analiza a mai multor variabile, atunci când se pune accent pe relația dintre variabila dependentă și una sau mai multe independente. Mai precis, analiza de regresie ne ajută să înțelegem modul în care valoarea tipică a variabilei dependente, în cazul în care una dintre variabilele independente este modificată, în timp ce celelalte variabile independente sunt fixe a avut loc.

În toate cazurile, scorul țintă este o funcție a variabilelor independente apelată funcția de regresie. Analiza de regresie, de asemenea, modificări caracteristice interesante ca variabila dependentă, funcția de regresie, care poate fi descrisă de o distribuție de probabilitate.

Analiza de regresie Sarcini

Această metodă statistică de cercetare este utilizat pe scară largă pentru a prezice momentul utilizării sale are avantaje semnificative, dar poate duce uneori la relație iluzie falsă sau de aceea este recomandat să utilizați cu exactitate în această chestiune, deoarece, de exemplu, corelația nu implică cauzalitate.

Acesta a dezvoltat un număr mare de metode pentru realizarea unei analize de regresie, cum ar fi regresia lineară și mai mici pătrate, care sunt parametrice. Esența lor este că funcția de regresie este definită în termenii unui număr finit de parametri necunoscuți, care sunt estimate din datele. Funcția de regresie neparametrică permite să se întindă într-un anumit set de funcții care pot fi infinit-dimensionale.

Ca o metodă statistică pentru studierea, analiza de regresie în practică depinde de procesul de generare a datelor forma și modul în care aceasta se referă la abordarea de regresie. Deoarece adevărata formă de date de proces, generând, de regulă, un număr necunoscut, analiza de regresie de multe ori depinde într-o anumită măsură, pe ipoteze cu privire la procesul. Aceste ipoteze sunt uneori verificabile dacă există suficiente date disponibile. Modelele de regresie sunt adesea utile chiar și atunci când ipotezele sunt încălcate moderat, cu toate că acestea nu pot funcționa la eficiență maximă.

Într-un sens mai restrâns de regresie se pot referi în mod specific la estimarea variabilelor de răspuns continue, în contrast cu variabilele de răspuns discrete utilizate în etichetare. Cazul variabilă continuu de ieșire este numit, de asemenea, regresia metrice, pentru a se distinge de probleme legate.

Termenul „regresie“ Francis Galton a inventat în secolul al XIX-lea pentru a descrie un fenomen biologic. Ideea a fost că creșterea descendenților strămoșii de creștere au tendința de a regresa până la media normală. Pentru regresie Galton a avut doar acest sens biologic, dar mai târziu lucrarea sa a fost continuată Udni Yoley și Karlom Pirsonom și retras la contextul statistic mai general. În lucrarea de Yule și Pearson distribuția în comun a variabilelor explicative și răspunsul este considerat a fi Gauss. Această propunere a fost respinsă de Fisher în lucrările din 1922 și 1925. Fisher a sugerat că distribuția condiționată a variabilei de răspuns este Gaussian, dar distribuția în comun nu trebuie să fie. În legătură cu această ipoteză Fischer mai apropiată de formularea din 1821 Gauss. Înainte de 1970, uneori, a durat până la 24 de ore pentru a obține rezultatele analizei de regresie.

Metode de analiză de regresie rămân zona activă a cercetării. În ultimele decenii, au fost dezvoltate noi metode de regresie fiabile; regresie cu răspunsurile corelate; Tehnici de regresie acomodarea diferitelor tipuri de date care lipsesc; regresie neparametrică; metode de regresie Bayesian; regresie, în care eroarea de măsurare predictivă variabilelor; Regresia cu cele mai multe dintre predictori decât observații și inferență cauzală cu regresie.

modele de regresie

Modele de analiză de regresie includ următoarele variabile:

• Necunoscute Parametrii marcați ca beta, care poate fi un scalar sau vector.
• variabile independente, X.
• Variabila dependentă, Y.

În diferite domenii ale științei, în cazul în care se realizează utilizarea analizei de regresie, diferiții termeni utilizează variabile în loc dependente și independente, dar în toate cazurile modelul de regresie se referă la X și Y funcția p.

Aproximarea se face de obicei în formă de E (Y | X) = F (X, β). Pentru a efectua analiza de regresie trebuie să fie determinată forma funcției f. Mai puțin frecvent, se bazează pe cunoașterea relației dintre Y și X, care nu se bazează pe date. În cazul în care astfel de cunoștințe nu este disponibilă, selectați forma flexibilă și convenabilă de F.

Variabilă dependentă Y

Să presupunem acum că vectorul parametrilor necunoscuți β are lungimea k. Pentru a efectua analiza de regresie, utilizatorul trebuie să furnizeze informații cu privire la Y variabilă dependentă:

• Dacă există N puncte de date ale formularului (Y, X), unde N

• Dacă există exact N = K, iar funcția F este liniară, ecuația Y = F (X, β) pot fi rezolvate exact, nu aproximative. Acest lucru reduce la rezolvarea unui set de ecuații cu N-N-necunoscutelor (elementele P), care are o soluție unică atâta timp cât X este liniar independent. În cazul în care F este o neliniară, soluția nu poate exista, sau pot exista mai multe soluții.
• Cea mai frecventă situație este în cazul în care există este N> punct la date. În acest caz, nu există suficiente informații în datele pentru a evalua valoarea unică pentru β, care se potrivește cel mai bine datele, precum și un model de regresie în cazul în care datele aplicației pot fi considerate ca un sistem de β supradeterminat.

În acest din urmă caz, analiza de regresie furnizează instrumente pentru:

• Căutarea soluțiilor de parametrii necunoscuți beta, care, de exemplu, pentru a minimiza distanța dintre măsurată și valoarea estimată a Y.
• În anumite ipoteze de analiză de regresie statistică folosind un exces de informații pentru a furniza informații statistice despre parametrii necunoscuți p și valorile estimate ale variabilei Y. dependente

Numărul necesar de măsurători independente

Luați în considerare modelul de regresie care are trei parametri necunoscuți: β0. β1 și β2. Să presupunem că experimentatorul efectuează 10 măsurători într-una și aceeași valoare a X. independent vector variabil în acest caz, analiza de regresie nu oferă un set unic de valori. Cel mai bun care se poate face pentru a estima media și deviația standard a variabilei Y. dependentă într-un mod similar, prin măsurarea două valori diferite ale lui X, se pot obține date suficiente pentru regresie cu două necunoscute, dar nu pentru trei sau mai multe necunoscute.

Dacă măsurătorile experimentator efectuate la trei valori diferite ale vectorului X variabilă independentă, analiza de regresie oferă un set unic de scoruri pentru cei trei parametri necunoscuți p.

În cazul situația generală de regresie liniară este echivalentă cu cerința de mai sus rezultă că matricea X T X reversibil.

ipoteze statistice

Când numărul de măsurători N este mai mare decât numărul de parametri necunoscuți k și măsurătorile de eroare εi. ea se extinde, de obicei, atunci informațiile conținute în exces măsurătorile, și este utilizat pentru predicțiile statistice despre parametrii necunoscuți. Acest exces de informație se numește gradul de libertate al regresiei.

ipotezele care stau la baza

ipoteze clasice pentru analiza de regresie includ:

• Eșantionul este reprezentativ pentru predicție inferență.
• Eroarea este o variabilă aleatoare cu o valoare medie zero, care este condiționată de variabilele explicative.
• Variabilele independente sunt măsurate fără erori.
• Variabilele independente (predictori) sunt liniar independente, adică nu este posibil de a exprima orice predictor ca o combinație liniară a celorlalte.
• Erorile sunt necorelate, adică matricea de covarianță este eroarea diagonală și fiecare element nenul sunt varianța erorii.
• varianța erorii este constantă din observațiile (homoscedasticity). Dacă nu, puteți utiliza mai mici pătrate sau alte metode, ponderat.

Acestea sunt condiții suficiente pentru estimarea celor mai mici pătrate au proprietățile necesare, în special, acele ipoteze înseamnă că estimările parametrilor sunt imparțiale, coerente și eficiente, în special atunci când acestea sunt înregistrate în clasa estimatorilor liniare. Foarte important, dovada este rareori satisface. Adică, este utilizată metoda, chiar dacă ipoteza nu este corectă. Variația ipotezelor pot fi folosite, uneori, ca o măsură de modul în care arată acest model este util. Multe dintre aceste ipoteze pot fi relaxate în tehnici mai avansate. Rapoartele de analiză statistică includ de obicei analiza probelor în conformitate cu modelul metodologie și utilitate.

În plus, variabilele în unele cazuri se referă la valorile măsurate în locațiile punctelor. Pot exista tendințe spațiale și autocorelație spațială în variabilele care încalcă ipotezele statistice. regresie ponderată geografică - singura metodă care are de a face cu datele.

Analiza de regresie liniară

În funcție de regresie liniară este că variabila dependentă, care este Yi. Reprezintă o combinație liniară a parametrilor. De exemplu, se utilizează un procedeu simplu de modelare de regresie liniară n puncte, o variabilă independentă, xi. și doi parametri, β0 și β1.

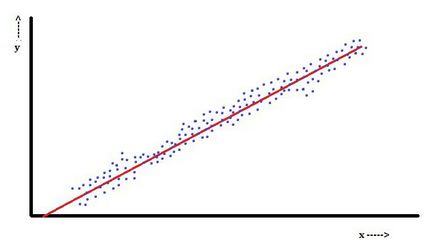
În regresie liniară multiplă, există mai multe variabile sau funcții independente.

Atunci când un eșantion aleatoriu din populația parametrii săi permite obținerea unui eșantion de un model de regresie liniară.

În acest aspect, cel mai popular este metoda celor mai mici pătrate. Cu ea a obținut parametri de evaluare care să reducă suma la pătrat reziduale. Acest tip de minimizare (caracteristică este regresia liniară) a acestei funcții conduce la un set de ecuații normale, și un set de ecuații liniare cu parametri care sunt rezolvate pentru a obține estimări ale parametrilor.

Cu în continuare ipoteza că populația este distribuită în mod normal, de eroare, cercetătorul poate utiliza aceste estimări ale erorile standard pentru crearea de intervale de încredere și a testa ipoteze cu privire la parametrii săi.

Analiza de regresie nelineară

Un exemplu în care funcția este neliniară în ceea ce privește parametrii, indică faptul că suma pătratelor să fie minimizată folosind o procedura iterativă. Se face o mulțime de complicații, care determină diferențele dintre metoda non-liniară mai mici pătrate și liniare. Prin urmare, rezultatele analizei de regresie folosind metoda neliniară uneori imprevizibile.

Calcularea puterii și a eșantionului dimensiunea

Aici, de regulă, nu există metode convenite cu privire la numărul de cazuri în comparație cu numărul de variabile independente din model. Prima regulă a fost propusă bună și Hardin și arată ca N = t ^ n, unde N este mărimea eșantionului, n - numărul de variabile independente, și t este numărul de observații necesare pentru a obține precizia dorită, în cazul în care modelul a avut doar o singură variabilă independentă. De exemplu, un cercetător construiește un model de regresie liniară, folosind un set de date care conține 1000 de pacienți (N). În cazul în care investigatorul decide că necesită cinci observații pentru a indica linia (m), numărul maxim de variabile independente, care modelul poate sprijini este 4.

alte metode

În ciuda faptului că parametrii modelului de regresie este de obicei estimată folosind metoda celor mai mici pătrate, există și alte metode care sunt utilizate mult mai puțin frecvent. De exemplu, sunt următoarele metode:

• Tehnicile Bayesian (de exemplu, Bayesian metodă de regresie liniară).
• regresie de interes sunt utilizate pentru situațiile în care o scădere a interesului erorilor este considerată mai adecvată.
• Cea mai mică deviație absolută, care este mai stabilă în prezența emisiilor, ceea ce duce la regresie quantile.
• regresie neparametrică, care necesită un număr mare de observații și calcule.
• Distanța metrici de învățare, care este studiat în căutarea pentru o distanță metrică semnificativă în spațiul de intrare specificat.

software-ul

Toate pachetele majore de software statistice sunt realizate folosind cel puțin analiza de regresie pătrate. regresie liniară simplă și analiza de regresie multiplă poate fi utilizat în anumite aplicații, foi de calcul, precum și pe unele calculatoare. Deși multe pachete de programe statistice pot efectua diferite tipuri de non-parametrice și regresie robuste, aceste metode sunt mai puțin standardizate; Diverse pachete software pune în aplicare diferitele metode. software-ul de regresie de specialitate a fost dezvoltat pentru a fi utilizat în domenii cum ar fi analiza sondajului și neuroimagistice.