Care sunt zero-uri și care este intervalele funcției studopediya semn constant

Luați în considerare o funcție.

1) Punctele la care graficul intersectează axa. numitele zerouri. Pentru a găsi zerourile funcției necesare pentru a rezolva ecuația. că este, găsiți valorile lui „X“. la care funcția dispare. Următorul exemplu ipotetic zerouri de funcții sunt indicate prin puncte roșii:

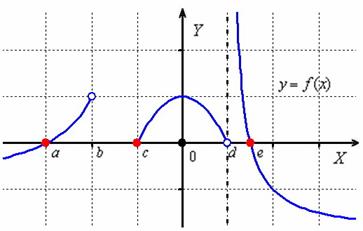
Este evident că. Rețineți că punctul nu este funcția de zero, din moment ce nu face parte din domeniul de definiție.

2) Intervalul de semn constant - este intervalul de timp în care fiecare punct este pozitiv sau negativ.

În cazul nostru, suntem pozitiv asupra intervalului. adică, pentru orice valoare a „X“ din oricare dintre intervalele de mai sus inegalitatea strict. Sau pur și simplu - graficul functiei la aceste intervale sunt situate deasupra axa x.

La intervale de funcții este negativă, adică orice valoare „X“, aparținând acestor intervale corespunde unei inegalități stricte. și o funcție de program este situat sub axa.

Rezultatele compact al acestor fapte este după cum urmează:
. în cazul în care;
. în cazul în care.
Șiruri pot fi rearanjate în unele locuri, nu contează, am folosit personal pentru a indica intervale de la început, ceea ce este pozitiv.

Ce se poate spune despre gama. Numai că nu este definită în acest interval, și, desigur, despre constanța semn de exprimare nu merge deloc.

Notă. în matematică este mai larg termenul de „decalaj“, care include nu numai intervalul, dar intervalul sau segment. Intervale și intervale de conectare constantă a constatat de multe ori functiile ukusochno-definite. În special, în cazul în care la figura de mai sus, punctul de „vopsea“ cu abscisă, obținem intervalul (în acest caz - intervalul) de semn constant. Dar va continua să fie considerate funcții „normale“ cu doar intervale de semn constant, astfel încât termenul de „perioada de semn constant“ nu are nevoie de speciale.