Care sunt zero-uri și cum să le identifice
Care sunt zerouri? Răspunsul este destul de simplu - este un termen matematic, prin care se înțelege domeniul unei funcții date, în cazul în care valoarea sa este zero. Zeros este numit, de asemenea, rădăcinile ecuației. Cel mai simplu mod de a explica ce zerouri, câteva exemple simple.
Să considerăm simplu ecuația y = x + 3. Deoarece funcțiile de la zero - valoarea argumentului, care au dobândit la zero, înlocuim 0 în partea stângă a ecuației:
În acest caz, este dorită -3 zero. Pentru această funcție, există doar o singură rădăcină a ecuației, dar nu este întotdeauna.
Luați în considerare un alt exemplu:
Înlocuim 0 în partea stângă a ecuației, la fel ca în exemplul anterior:
Evident, în acest caz, zerouri va fi de două x = 3 și x = -3. Dacă în ecuația a fost argumentul celui de al treilea grad, trei zerouri au fost ca. Puteți trage o concluzie simplă că numărul de rădăcini ale unui polinom este gradul maxim al argumentului său în ecuația. Cu toate acestea, mai multe funcții, cum ar fi y = x 3 par să contrazică această afirmație. Logica și bunul simț sugerează că această funcție este doar un singur zero - punctul x = 0. Dar, de fapt, rădăcinile de trei, acestea sunt toate la fel. Dacă vom rezolva ecuația într-o formă complexă, devine evident. x = 0, în acest caz, rădăcină, multiplicitate 3. In exemplul anterior, sunt zerouri nu coincid, deoarece unul a avut multiplicitate.
algoritmul de determinare
Din aceste exemple arată modul de determinare a zerouri. Algoritmul este mereu același:
- funcția de înregistrare.
- Substitut y sau f (x) = 0.
- Rezolva ecuația rezultată.
Complexitatea ultimului punct depinde de gradul ecuației argumentului. La decizia de gradul ridicat al ecuației este deosebit de important să ne amintim că numărul de rădăcini ale ecuației este egală cu gradul maxim al argumentului. Acest lucru este valabil mai ales pentru ecuatii trigonometrice, unde cele două porțiuni de diviziune prin sinus sau cosinus duce la pierderea de rădăcini.
Ecuațiile de grad arbitrar este cel mai ușor rezolvată prin Horner, care a fost proiectat special pentru a găsi zerouri ale unui polinom arbitrar.
Valoarea zerourilor poate fi fie negativ sau pozitiv, real sau situată în planul complex, unice sau multiple. Sau rădăcinile pot să nu fie. De exemplu, funcția y = 8 nu va primi zero pentru orice x, deoarece nu depinde de această variabilă.
Ecuația y = x 2 -16 are două rădăcini, și ambele se află în planul complex: 4і x1 = x2 = -4і.
greseli frecvente
O greșeală comună că elevii încă nu au dat seama multe despre ceea ce este zero - se înlocuiește cu zero argument (e) și nu funcția de valoare (y). Ei au pus încredere în ecuația x = 0 și, pe această bază, sunt la. Dar aceasta este o abordare greșită.
O altă eroare, după cum sa menționat deja, reducerea sinus sau cosinus în ecuații trigonometrice, din cauza a ceea ce este pierdut, și unul sau mai multe zerouri. Acest lucru nu înseamnă că aceste ecuații nu pot tăia nimic, doar atunci când alte calcule trebuie să ia în considerare aceste „pierdute“ factori.
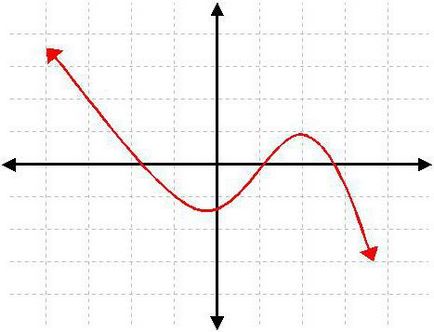
Reprezentarea grafică
Înțelegeți ce zerourile, puteți utiliza programe matematice, cum ar fi Maple. Este posibil să se construiască un grafic care indică numărul dorit de puncte și scara dorită. Aceste puncte la care graficul traversează axa x este zerouri necesare. Aceasta este una dintre cele mai rapide moduri de a găsi rădăcinile unui polinom, mai ales în cazul în care este mai mare decât al treilea ordin. Deci, dacă există o nevoie de a efectua în mod regulat calcule matematice, pentru a găsi rădăcinile polinoame de puteri arbitrare, vă construi program, Maple sau un program similar este pur și simplu indispensabil pentru implementarea și verificarea calculelor.
