Cum de a rezolva ecuația cu un modul

Ecuația cu un modul (valoare absolută) este orice ecuație în care variabila sau expresia este închisă într-un corset modular. Valoarea absolută a lui x este notat cu | x | . iar modulul este întotdeauna pozitiv (cu excepția zero, ceea ce nu este nici pozitiv, nici un număr negativ). Ecuația este rezolvată cu valoarea absolută ca orice altă ecuație matematică, dar ecuația cu modulul poate avea două din rezultatul final, deoarece este necesar să se rezolve ecuația de pozitive și negative.

pași Editare

Partea 1 din 3: Înregistrarea Editați ecuația

Înțelegerea conceptului de valoarea absolută a unui punct de vedere geometric. Numărul modulului este egală cu distanța dintre originea și numărul respectiv. [2] Modulul este desemnat citate modulare, în care este un număr, variabilă sau expresie (| x |). Numărul modulului este întotdeauna pozitiv. [3]

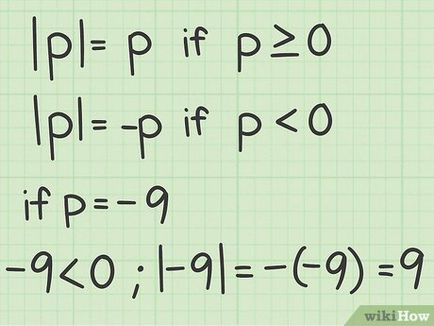
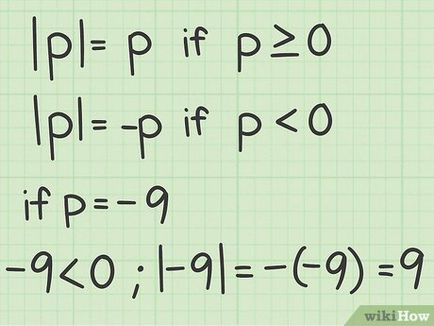
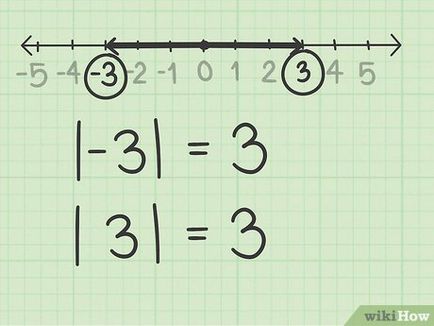
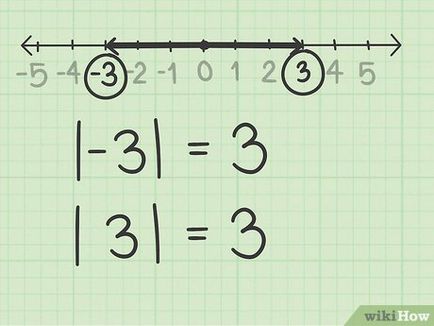
• De exemplu, | - 3 | = 3 | 3 | = 3. Ambele numere -3 și 3 sunt la o distanță de trei unități de la 0 ° C.

În ecuația, izola modulul. Mărimea absolută ar trebui să fie pe o parte a ecuației. Orice număr sau membri este între paranteze modulare trebuie deplasat către cealaltă parte a ecuației. [4] Rețineți că unitatea nu poate fi setat la un număr negativ, așa că, dacă după modul de izolare, acesta este un număr negativ, această ecuație nu are nici o soluție. [5]

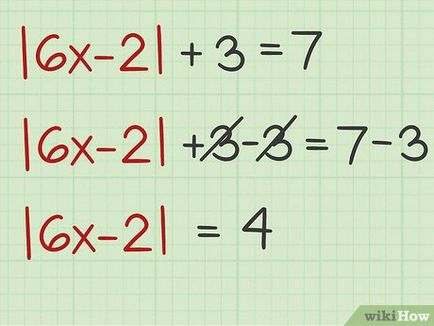
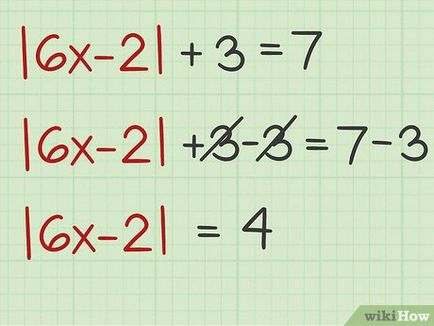
• De exemplu, având în vedere ecuația | 6 x - 2 | + 3 = 7; pentru a izola aparatul de ambele părți ale ecuației, scade 3:
  | 6 x - 2 | + 3 = 7
  | 6 x - 2 | + 3 - 3 = 7-3
  | 6 x - 2 | = 4

Verificați rezultatul unei soluții pozitive a ecuației. Pentru această valoare obținută pentru a substitui în ecuația inițială [8]. că este, substitui valoarea lui x. a constatat ca urmare a soluțiilor pozitive ale ecuației în ecuația originală cu modulul. În cazul în care egalitatea dreptului de decizie.

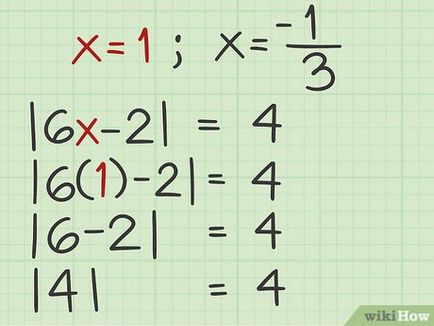
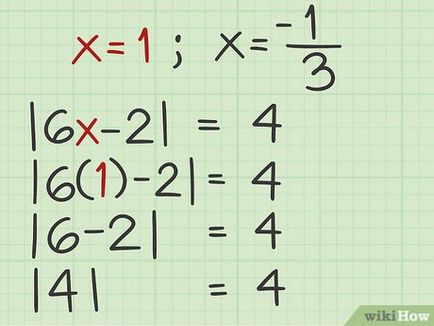
• De exemplu, în cazul în care, ca urmare a soluției pozitive a ecuației veți găsi că x = 1. înlocuirea în ecuația originală 1:
  | 6 x - 2 | = 4
  | 6 (1) - 2 | = 4
  | 6 - 2 | = 4
  | 4 | = 4

Verificați rezultatul deciziei negativă a ecuației. În cazul în care una dintre soluțiile este corectă, aceasta nu înseamnă că a doua decizie este corectă. Prin urmare, pentru a substitui valoarea lui x. găsită prin rezolvarea ecuației negative, în ecuația originală cu modulul.

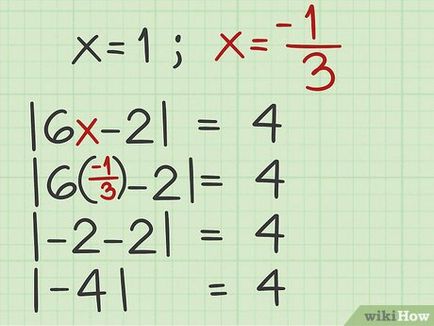
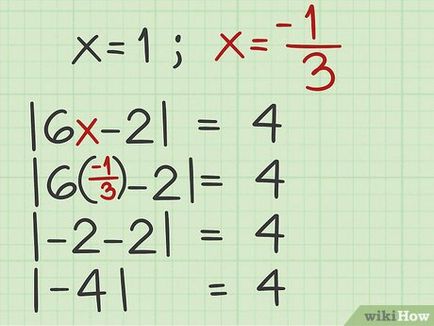
• De exemplu, în cazul în care, ca urmare a deciziei negative a ecuației veți găsi că x = - 1 martie >>. substitut - 1 3 >> în ecuația originală:
  | 6 x - 2 | = 4
  | 6 (- 1 3) - 2 | = 4>) - 2 | = 4>
  | - 2 - 2 | = 4
  | - 4 | = 4

Să acorde o atenție la soluții reale. Soluția ecuației este validă (adevărat), în cazul în care înlocuirea în ecuația inițială se observă ravenstvo.Imeyte cont de faptul că ecuația poate avea două, una sau nici o soluție reală.

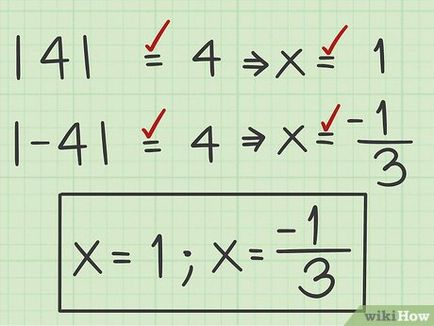
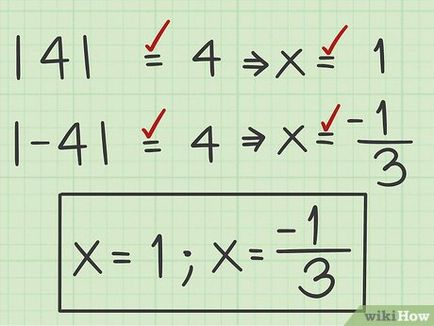
• În acest exemplu, | 4 | = 4 și | - 4 | = 4. adică, egalitatea ambelor soluții sunt valabile. Astfel, ecuația | 6 x - 2 | + 3 = 7 are două soluții posibile: x = 1. x = - 1 martie >>.