Divizarea cercul pentru orice număr de părți egale
Termenii de construcții circumferinței
cerc închis se numește o curbă, din care fiecare punct este echidistant față de un punct O, numit centru.
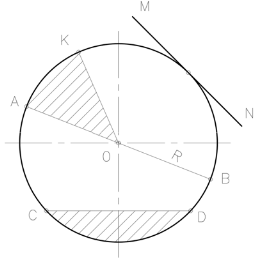
Liniile drepte care leagă orice punct al cercului cu centrul său se numește raza R. Direct AB care leagă două puncte ale cercului și care trece prin centrul său O, numită diametrul D. Partea cercului se numesc arce. Direct CD, care leagă două puncte de pe cerc se numește o coardă. Direct MN, care are doar un singur punct comun cu cercul se numește tangentă. O parte dintr-un cerc mărginit de o coardă și un CD cu arc este numit sigmente. O parte dintr-un cerc delimitat de două raze și un arc este numit un sector. Două linii reciproc perpindikulyarnye orizontale și verticale care se intersectează în centrul cercului, numit axa cercului. Unghiul format de două raze se numește KOA un unghi central. Două perpendiculare reciproc rază 90 formează un unghi de 0 și 1/4 limită cerc.
Despartitor circumferențial 4-D și 8-NIL părți identice
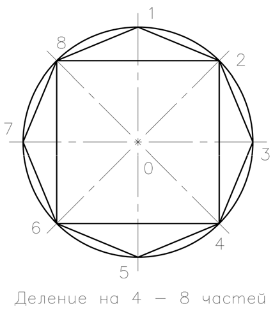
Desenați un cerc cu axele orizontale și verticale, care se împarte în 4 părți egale în D. Efectuate cu un șubler sau cu 450 gon, două linii perpendiculare împart cercul în 8 părți egale NIL.
Divid cercul 3 și 6 părți egale (trei multipli de 3)
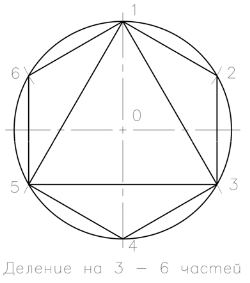
Pentru a împărți circumferința de 3,6 ori și să le transporte la numărul de piese și circumferința unei axe corespunzătoare ale razei predeterminate. Divizarea poate porni de la punctul de intersecție al axei orizontale sau verticale, cu circumferința. Raza predeterminată a cercului secvențial întârziat 6 de cinci ori. În continuare, aceste puncte de pe cerc conectate succesiv prin linii drepte, pentru a forma un adevărat test șase poligon inscris. La punctele de conexiune printr-o dă un triunghi echilateral, și împărțiți circumferința în trei părți egale.
Divizarea cercul la 5 și 10 să fie cinci părți egale
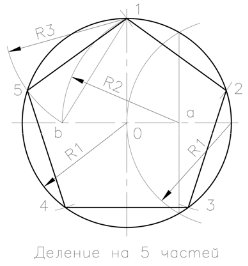
Construirea unui pentagon regulat, după cum urmează. Desenați două axe perpendiculare între circumferința egală cu diametrul cercului. Se împarte jumătatea dreaptă a jumătate din diametrul orizontal prin arc R1. Din punct obținut „o“ în mijlocul acestui interval de rază R2 care efectuează arc de cerc la intersecția cu diametrul orizontal la punctul „b“. Raza R3 de la punctul „1“ se realizează la intersecția unui arc de cerc cu o circumferință predeterminată (V.5) a condus direcția unui pentagon regulat. Distanța „b-On“, dă partea corectă a Decagon.
Despartitor Numărul circumferențial N-Noe unități identice (construirea unui poligon regulat al N laturi)
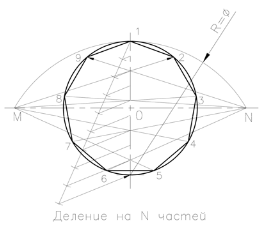
Acesta este după cum urmează. Atragem o axă orizontală și verticală sunt circumferința reciproc perpendiculare. Din punctul de sus „1“ cerc exploatație la un unghi arbitrar față de axa verticală a unei linii drepte. Amâne segmente egale de lungime arbitrară, egal cu numărul de părți la care se împarte această circumferință, de exemplu 9. Sfârșitul ultimului segment conectat la punctul inferior al diametrului vertical. Desenați linii paralele obținute din toate segmentele în așteptare până la intersecția cu un diametru vertical, împărțind astfel diametrul vertical al cercului de un număr predeterminat de părți. Raza egală cu diametrul circumferinței punctului inferior al axei verticale a arcului de susținere MN până la intersecția cu extinderea pe orizontală a axei cercului. Din punctele M și N care deține grinzi prin par (sau impare) al punctului de divizare diametrului vertical la cercul de intersecție. Rezultante segmente de cerc sunt de dorit, deoarece punctele 1, 2, .... 9 împart cercul în 9-Th (N) părți egale.
Găsirea centrul arcului
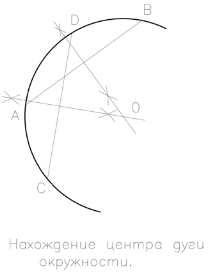
Pentru a găsi centrul circumferinței arc postraeniya efectuați următoarele: pentru o notă dată cu arc patru puncte arbitrare A, B, C, D și să le combine în perechi acorduri AB și CD. Fiecare dintre acorduri cu o busolă în jumătăți, având astfel o trecere perpendicular prin centrul coardei respective. Suprapunerea acestor perpendicularele dă centrul arcului și cercul corespunzător.