Divizarea circumferința în părți egale

Circumferința - planul locus al punctelor echidistante dintr-un anumit punct numit centru al unei nenulă distanță predeterminată, numită raza.

În acest articol vă va învăța cum să împartă circumferința de 3-6, 4-8, 5-10 și n părți.

Cum să împartă circumferința la 3 și 6 părți

Pentru a împărți cercul în 3, 6 și un număr multiplu de piese ținându-le cerc cu o rază predeterminată și este axa responsabilă. Divizarea poate porni de la punctul de intersecție al axei verticale sau orizontale a cercului. Raza predeterminată a cercului secvențial depus de 6 ori. În continuare, aceste puncte de pe cerc conectate secvențial prin linii drepte și formează un hexagon regulat inscris. puncte de conectare prin odnudaet triunghi echilateral, și care separă cercul în trei părți egale.

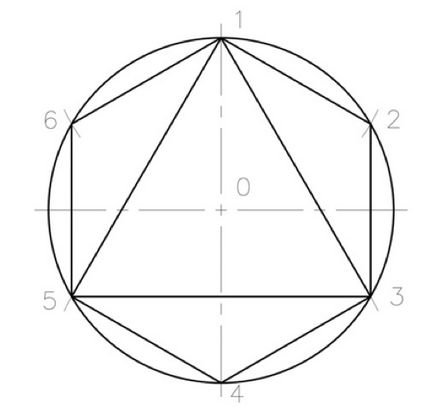
Divid părți egale circumferențial 3-6

Cum să împartă cercul în 5 și 10 părți

Pentru a împărți cercul în 5 și 10 părți egale necesare pentru a construi un pentagon regulat. Pentru construirea ei, se procedează după cum urmează. Desenați două axe perpendiculare între circumferința egală cu diametrul cercului. Se împarte jumătatea dreaptă a jumătate din diametrul orizontal prin arc R1. «B» din punctul obținut „o“ în mijlocul acestui interval de rază R2 care efectuează arc de cerc la intersecția cu diametrul orizontal la punctul. Raza R3 de la punctul „1“ se realizează la intersecția unui arc de cerc cu o circumferință predeterminată (Vol. 5) pentru a da partea unui pentagon regulat, și apoi pune distanța pe circumferință obținută de 5 ori pentru a obține pentagon regulat. Depărtarea «b-0" dă partea corectă a pentagonului.

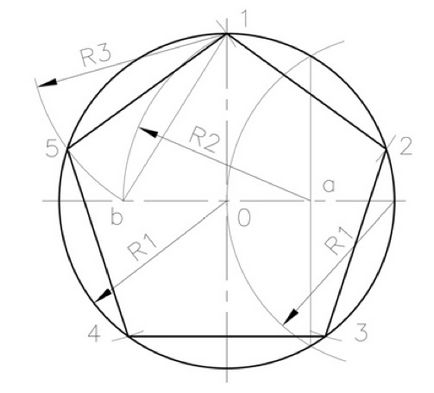
Despartitor circumferențiale 5-10 părți egale

Cum să împartă cercul în n - părți egale

În caz contrar, aveți nevoie pentru a construi un poligon regulat cu n numărul de laturi. Atragem o axă orizontală și verticală sunt circumferința reciproc perpendiculare. Din punctul de sus „1“ cerc exploatație la un unghi arbitrar față de axa verticală a unei linii drepte. Amâne segmente egale de lungime arbitrară, egal cu numărul de părți în care se împarte această circumferință, de exemplu 9. Sfârșitul ultimului segment conectat la punctul inferior al diametrului vertical. ele sârmă linii paralele cu capătul pregătit al segmentelor amânate să se intersecteze cu diametrul vertical, împărțind astfel diametrul vertical al cercului de un număr predeterminat de părți. Raza egală cu diametrul circumferinței punctului inferior al axei verticale a arcului de susținere MN până la intersecția cu extinderea pe orizontală a axei cercului. Din punctele M și N care deține grinzi prin par (sau impare) al punctului de divizare diametrului vertical la cercul de intersecție. Rezultante segmente de cerc sunt de dorit, t. K. Punctele 1, 2, ... 9 divide cercul 9 (N) părți egale.

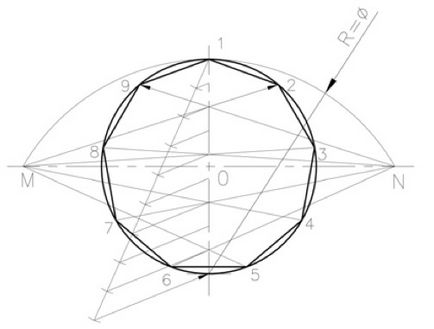
Despartitor circumferențial n părți egale

Divizarea circumferința unui număr arbitrar de părți egale pot fi produse folosind tabelul de coardă, o expresie numerică care se calculează prin înmulțirea raza cercului cu factorul corespunzător numărului de diviziune, cum se arată în tabel.

Tabelul polifonice (coeficienți pentru împărțirea cercului)

Numărul de diviziuni părți ale cercului