ecuaţia modulului
Interpretarea geometrică a modulului: este distanța de la punctul de 0 până la un punct situat pe axa de coordonate.
Să - o expresie algebrică. Apoi, folosind definiția modulului (9), în conformitate cu ipotezele corespunzătoare, putem dezvălui semnul valorii absolute a expresiei:
O ecuație care conține o expresie necunoscută x sub semnul modulului, denumit ecuația modulului.
Luați în considerare principalele tipuri de ecuații cu modul și metodele de soluțiile lor.
Să mai departe. . - unele expresii cu variabila x. și.
în cazul în care un - număr, - o expresie a x necunoscut.
1. În cazul în care. Ecuația (10) nu are nici o soluție.
2. În cazul în care. Ecuația (10) este echivalentă cu ecuația.
3. În cazul în care. Ecuația (10) set de ecuații este echivalent cu:
în cazul în care. - unele expresii ale x necunoscute.
Pentru a rezolva această ecuație în mai multe moduri.
1st capacitate folosind o definiție modul:
2a capacitatea folosind abordarea soluției a modului de ecuații de tip I, cu o condiție suplimentară privind semnul expresiei:
Notă: 1 st sau 2 Metoda II de rezolvare a acestor ecuații sunt selectate în funcție de care dintre inegalitățile sau rezolvate mai ușor.
intervale capabile de a treia metodă. trebuie:
1) Găsiți valorile lui x. pentru care
2) Se aplică valorile obținute x în axa reală;
3) determinarea semnelor pentru fiecare dintre benzile obținute;
4) tracta o mărci ale curbei;
5) pentru a rezolva ecuația pentru fiecare interval individual, dezvăluind modulul conform figurii;
6) pentru fiecare interval specific pentru a verifica dacă este sau nu rădăcini primite aparțin acestui interval;
7) în răspunsul pentru a indica totalitatea tuturor rădăcinilor primite.
Tip III: ecuații care conțin mai multe module. În cazul în care două dintre ele, atunci această ecuație este de forma:
în cazul în care. . . - unele expresii ale x necunoscute.
Prima modalitate - puteți utiliza definiția modulului și luate în considerare 4 cazuri de semne posibile. . Această metodă, de regulă, nu este rațional.
Metoda 2 -Metoda intervale. Este necesar să se atragă ca axe numerice și semne curbe mult ca module în ecuație. Pentru ecuația (11), trage cele două axe, plasându-le unul sub celălalt (o axă pentru al doilea. - To). Pentru fiecare expresie, și ar trebui să descrie curba mărcilor pe axa respectivă. Apoi, deschideți modulele folosind imaginea și de a rezolva ecuația separat pe fiecare interval. Adecvate numai acele rădăcini care aparțin perioadei în cauză. Ca răspuns, trebuie să specificați setul de rădăcini obținute.
Prima metodă - soluție a ecuației (12) se reduce la rezolvarea unui set de ecuații:
2a metoda intervalelor de abilitate (nu rațional).
Metoda A treia - după construirea ecuației în pătrat și de a folosi proprietățile modulului se reduce la ecuația este echivalentă cu:
Ecuația rezultată se rezolvă în funcție de tipul acestuia.
Tip V: ecuație rezolvată variabilă substitut, de ex
Prin proprietatea modulului este scris sub forma
Administrat de înlocuire și de a rezolva ecuația de gradul doi obținut în necunoscut. Apoi, aveți nevoie pentru a merge înapoi la variabila vechi. În cazul 2 rădăcini diferite ale ecuației pătratice este un set de ecuații este de tip I:
dacă rădăcina este singura care rămâne pentru a rezolva ecuația
Trebuie amintit că, în cazul unei valori negative ecuație cu modulul nu are soluții.
Această ecuație de tip I. TCC lui :.
Ecuația poate fi scrisă ca
. Pe DHS poate fi redus și obținem
potrivit pentru DHS.
Exemplul 2: rezolva ecuația.
Această ecuație de tip II. TCC lui :. Ea are o soluție în cazul în care. și anume la. Astfel, pentru a obține
Rezolvam primit separat ecuații raționale fracționare. Prima ecuație reduce de a avea
Aceasta este o ecuație de gradul doi nu are nici o soluție, deoarece .
Din al doilea set de ecuații (13) obținem
Ecuația pătratică are rădăcini:
Cu toate acestea, și anume prima rădăcină nu aparține. care a rezolvat ecuatia, răspunsul este doar.
De tip II au o ecuație care va decide cu privire la definirea modulului.
Rezolvarea sistemului primei pluralitatea (14):
Valoarea nu este adecvată pentru starea. Rămâne rădăcină.
Rezolvarea sistemului de a doua multitudine (14):
Exemplul 4. Rezolvați ecuația.
Deoarece. atunci ecuația poate fi scrisă ca
Această ecuație se referă la tipul ecuațiile III.
TCC lui :. Noi rezolva metoda de intervale.
Zerourile expresiei sub module sunt:
Aceste valori numerice sunt împărțite în trei axe spațiu.
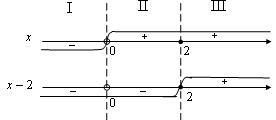
Extinderea unităților pe fiecare dintre lacunele care rezultă, ținând seama de mărcile lor, pentru a primi un set de sisteme:
Noi rezolva separat sistemul.