Elementele cheie ale triunghiului ABC

Nodurile - punctele A, B și C;

Party - lungimi a = BC, b = AC și c = AB, care leagă nodurile;

Unghiurile - a. β, y format din trei perechi de laturi. Unghiuri adesea menționată ca și partea de sus, - literele A, B și C.

Unghiul format de laturile triunghiului și situată în zona interioară, numit unghiul interior și adiacent acestuia este colț adiacent al triunghiului (2, p. 534).

Inaltime, mediana, bisectoare și linia mediană a triunghiului

Pe lângă elementele de bază ale triunghiului au în vedere alte segmente având proprietăți interesante: ridicate, mediana bisectoare linia isrednie.

Înălțimea triunghiului - este perpendiculară pe vârful unui triunghi pe partea opusă.

Pentru construirea de înălțime, se procedează după cum urmează:

1) trage o linie dreaptă care conține una dintre laturile triunghiului (dacă înălțimea vârfurilor se realizează un unghi ascuțit într-un triunghi obtuz);

2) din partea de sus, situată vizavi de linia trasată, pentru a efectua segmentul din punct de la această linie constituind cu ea un unghi de 90 de grade.

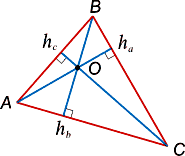
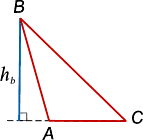
înălțimea punctului de intersecție cu latura triunghiului se numește înălțimea bazei (vezi. fig. 2).

altitudini Proprietăți ale unui triunghi

Într-un triunghi dreptunghic înălțimea trase din partea de sus a unghiului drept, se împarte în două triunghiuri similare cu triunghiul original.

Într-un triunghi-acută, înălțime două triunghiuri similare sale tăiat de la el.

În cazul în care un triunghi-acut, baza tuturor înălțimi aparțin laturi ale triunghiului, și triunghi obtuz în două înălțimi cad pentru a continua petrecerea.

Trei înălțime în triunghi acută se intersectează într-un punct, iar acest punct se numește orthocenter triunghiului.

Median (Mediana Latină -. «Mediu») - ea segmente care unesc vârfurile triunghiului cu punctele mediane ale laturilor opuse (a se vedea figura 3 ..).

Pentru a construi o valoare mediană urmați acești pași:

1) pentru a găsi mijlocul partidului;

2) conecta puncte, este punctul de mijloc lateral de triunghi, cu vârful segmentului opus.

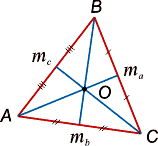
Proprietățile medianele triunghiului

Mediana împarte triunghiul în două triunghiuri de suprafață egală.

Medianele unui triunghi se intersectează într-un punct, care împarte fiecare dintre ele într-un raport de 2: 1, pornind de la partea de sus. Acest punct se numește centrul de greutate al triunghiului.

Total triunghi este împărțit în șase medianele lor de triunghiuri egale.

bisector

Bisectors (de bis latini -. De două ori „și seko - diseca) este chemat prizonierii din interiorul triunghiului segmentele de linie care bisect unghiurile sale (a se vedea figura 4 ..).

urmați acești pași pentru construirea bisectoarei:

1) pentru a construi raza care provine de la vârful unghiului și îl împarte în două părți egale (bisectoarea unghiului);

2) pentru a găsi intersecția bisectoarea unghiului triunghiului în partea opusă;

3) Aloca segment care leagă vârful triunghiului cu punctul de intersecție pe partea opusă.

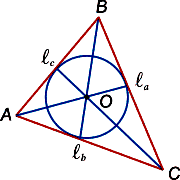
Bisectors triunghi Proprietăți

Bisector unghiul triunghi împarte latura opusă într-un raport egal cu raportul dintre două laturi adiacente.

De Bisectoarele unghiurilor interioare ale unui triunghi se intersectează la un moment dat. Acest punct este numit centrul cercului înscris.

De Bisectoarele unghiurilor interioare și exterioare sunt perpendiculare.

Dacă bisectoarea unghiului extern al triunghiului intersectează extensia partea opusă, apoi adbd = ACBC.

Bisectoarea unul intern și două unghiuri exterioare ale unui triunghi se intersectează la un moment dat. Acel punct - centrul unuia dintre cele trei cercuri ale triunghiului cum este descris.

Baze Bisectoarele două interne și una unghiurile externe ale minciunii triunghi pe o singură linie, dacă bisectoarea exterioară a unghiului nu este paralelă cu latura opusă a triunghiului.

Dacă bisector triunghi în afara colțuri nu sunt paralele cu laturile opuse, atunci bazele lor se află pe o singură linie.