Rădăcini și amploarea și proprietățile lor
Gradul este o expresie a formei: unde:
- - baza puterii;
- - exponent.
Gradul cu un indicator natural
Definiți indicele conceptului grad care - întreg (adică un număr întreg și pozitiv).
- Prin definiție :.
- Construiți număr într-un pătrat - apoi se multiplica de la sine:
- Construiți număr în cub - apoi înmulțiți-l de la sine de trei ori.
Construiți număr la o putere naturală - apoi multiplica numărul de la sine din nou:
Gradul cu o măsură de
Dacă exponentul este un număr întreg pozitiv:
Construcția de gradul zero:
Dacă exponentul este un număr întreg negativ:
Notă: Expresia nu este definită, în cazul n ≤ 0. Dacă n> 0. atunci
Gradul cu exponent rațional
Arithmetic rădăcină pătrată
Ecuația are două soluții: x = 2 și x = -2. Acesta este numărul a cărui pătrat este egal cu 4.
Luați în considerare ecuația. Desenați un grafic al funcției și a vedea că are două soluții, unul pozitiv, celălalt negativ.
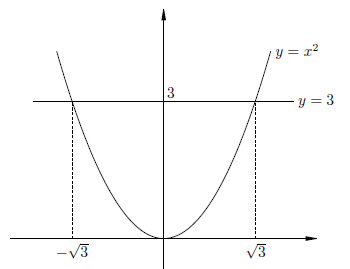
Dar, în acest caz, soluțiile nu sunt numere întregi. Mai mult decât atât, ele nu sunt raționale. Pentru a înregistra aceste decizii iraționale, vom introduce un simbol special al rădăcinii pătrate.
Aritmetică rădăcină pătrată „/> - este un număr non-negativ al cărui pătrat este egal cu, o ≥ 0. Atunci când un <0 — выражение " /> Nu a fost determinat pentru că nu există nici un număr real al cărui pătrat este un număr negativ.
rădăcina pătrată
De exemplu, 20% = 202% "/>. O soluție a ecuației, respectiv" /> și „/>
cub-rădăcină
Rădăcina cub de numărul - un număr care este egal cu cubul. Rădăcina cub este definit pentru toți. Acesta poate fi eliminat din oricare dintre:% 20,% = 20-2 „/>.
Rădăcina gradul n-lea
rădăcină de putere Th a numărului - un număr care este egal cu puterea de mii.
În cazul în care - chiar.
- Apoi, în cazul în care un <0 корень n -ой степени из a не определен.
- Sau dacă o ecuație aritmetică ≥ 0. rădăcină atunci nenegative se numește n-lea rădăcină al unui grad și este notat „/>
În cazul în care - este ciudat.
- Apoi ecuația are o singură rădăcină pentru fiecare.