Rhombus, trapez - studiul temelor - poligoane - în curs de geometrie școală
În manualul LS „Geometrie 7-9“ Atanasyan (4) Termenul „diamant“ este introdus în §3 revendicarea 46 „Diamond și Piața“: Rhombus este numit un paralelogram în care toate părțile sunt egale. o revizuire și dovedesc proprietatea rhombus: „diagonalele unui romb sunt perpendiculare și împărțiți-l în două colțuri.“
AV Pogorelov (18) tema „diez“ identifică un anumit element (55).
La începutul paragrafului definește: Rhombus - un paralelogram în care toate părțile sunt egale. Și apoi intră în proprietatea romburi ca Teorema 6.5: „diagonalele unui romb se intersectează în unghiuri drepte. Diagonalele unui romb sunt Bisectoarele unghiurilor sale. "
AC, BD - în diagonală.
AC, BD - bisector.
AABC - isoscel, pentru că AB = BC (ABCD-diamant).
AO = sistem de operare (de proprietatea unui paralelogram) => IN - Median, a => și bisectoarea, și înălțimea.
Deci, BD - mediatoare B și perpendicular pe UA.
Luați în considerare metoda de a studia tema „Diamond“, la un exemplu de manual de AV Pogorelov.
După introducerea proprietăților și definițiile elevilor diez rezolva probleme.
Sarcina 1. Dovedește că în cazul în care diagonalele unui paralelogram sunt perpendiculare, atunci este un romb.
Având în vedere: ABCD-paralelogram, AC, BD-diagonala, ACBD.
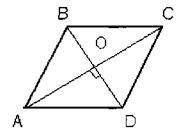
Să Despre - punctul de intersecție al diagonalelor. # 63; AOB = # 63; OCD (pe baza I), AOB = OCD = 90 (prin ipoteză) OA - general, OB = OD (proprietatea diagonalelor paralelogramului).
=> AB = AD. Și pe proprietate laturile opuse ale paralelogramului AD = BC, AB = CD.
3adacha 2. Perimetru romburi ABCD este 56cm. Găsiți colțuri diez (oral).
3adacha 3. Unul dintre colțurile rombului este egal cu 72. ABCD obține colțuri diez (oral).
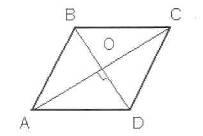
Răspuns: A = C = 72, B = D = 108.
Apoi, ei pot oferi sarcini de sistem:
1. pilulă ABCD ținut AC diagonală. Demonstrati ca triunghiul ABC - isoscel.
2. Două cercuri centrate la O și O1 raze egale și se intersectează în punctele A și B. Arată că VO AO1 patrulater - paralelogram.
3. romburi Side este 18cm, iar unul dintre unghiurile este egal cu 150 obține distanța dintre laturile sale opuse.
4. Dovedește că punctul de intersecție al diagonalelor unui romb este echidistant față de laturile sale.
În manualul „Geometrie 7-11“ AV Pogorelov (18) tema "A-Line" este studiată în §6 revendicarea 59 "Trapeze". Determinarea trapezului este introdusă în nachalepunkta: Trapezium se numește patrulateră, în care numai două laturi opuse sunt paralele. Aceste laturi paralele sunt numite baze ale unui trapez. Celelalte două părți sunt numite flancurilor.
Următorul a introdus conceptul de „isoscel trapezoid“ și „linia de mijloc a trapezului“ si este considerata Teorema 6.8 (pe linia mediană a trapezului): „Linia de mijloc paralelă cu bazele trapezului și este egală cu jumătate din suma dintre ele.“
În manualul LS „Geometrie 7-9“ Atanasyan (4) termenul „trapezului“ este introdus în §2 «paralelogram și trapez“, la punctul 44 din «A-line»:
„KEYSTONE numit patrulateră, în care cele două părți sunt paralele, celelalte două părți nu sunt paralele. laturile paralele ale trapezului sunt numite bazele sale, iar celelalte două laturi - laturile.
Trapez isoscel numit în cazul în care laturile sale sunt egale. Trapez, dintre care un colț este o linie dreaptă, numit pătrat. "
Luați în considerare metoda de a studia tema „Keystone“ pe exemplul manual de AV Pogorelov.
Trapeze numit patrulater, ale cărei doar două laturi opuse sunt paralele. Aceste laturi paralele sunt numite baze ale unui trapez. Celelalte două părți sunt numite flancurilor.
Prezentată aici este un ABCD trapez cu bazele AB și CD și BC și AD părțile laterale.
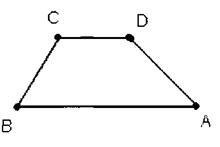
Trapez, care se numesc laturile unui echilateral. Segmentul care conectează mijlocul laturilor, se numește linia de mijloc a trapez.
Teorema 6.8: Mijlocul linie paralelă cu bazele trapezului și este egală cu jumătate din suma acestora.
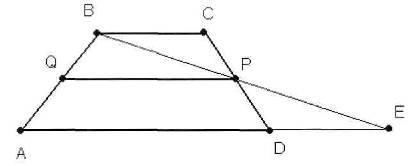
BP # 63; AD = E, # 63; PBC = # 63; PED (în conformitate cu cea de a doua caracteristică a egalității de triunghiuri) CP = DP (de construcție), PCB = PDE (intern culcat în cruce cu linii paralele BC și AD și CD-ul de tăiere), BPC = EPD (vertical).
Din egalitatea de triunghiuri => = PB PE, BC = ED.
Deci, linia de mijloc PQ este linia centrală a trapezului # 63; AVE. Conform proprietăților liniei medie a triunghiului PQ || AE și segmentul
= PQ # 63; AE = # 63; (ad + bc).
După introducerea conceptelor de mai sus elevii să rezolve probleme.
Zadacha1. În colțuri ABCD trapez adiacente latura AD, sunt 74 și 81. Se determină unghiurile adiacente latura Soarelui (Oral).
Raspuns: ABC = 106, BCD = 99.
Zadacha2. Demonstrati ca o echilaterale unghiurile trapezoizi la baza sunt egale.
Având în vedere:-ABCD trapez isoscel,
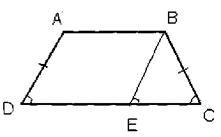
BP || AD, ABED - paralelogram => BE = AD (de proprietatea unui paralelogram) AD = BC (prin ipoteză) => # 63; ALL - baza de isoscel-UE. Colțurile triunghiului și trapezului la nodul C sunt aceleași, iar unghiurile de la vertex E și D sunt ambele la intersecția colțurilor respective ale intersectând linii paralele. Prin urmare, ADC = BCD.
Apoi, elevii pot oferi sarcini de sistem care vizează dezvoltarea abilităților relevante.
1. Într-un echilaterale colțuri ABCD trapez adiacente laterale AD, egală cu 45. Găsiți înălțimea trapezoid, dacă baza sunt de 13 cm și 27 cm.
Dovedește că în cazul în care diagonalele sunt egale cu trapez, trapez este isoscel.
In trapez, unul dintre motivele care este egală cu 5 cm a avut loc linia de mijloc, a cărei lungime este egală cu 6 cm. Care este cealaltă bază trapezului?
Diagonalele intersectează linia medie RP trapez ABCD la punctele M și N. Dovedeste ca RM = NP.
Demonstrați că punctele de centru ale unui trapez echilateral sunt nodurile unui romb.
Lecții Sinopsis pe „trapez. Linia de mijloc a trapezului "
Educație: consolidarea cunoștințelor proprietăților studiate ale trapezului și teorema pe linia mediană a trapezului, trapez preda pentru a stabili condițiile de existență; să învețe cum să aplice formula de a găsi linia de mijloc a trapezului la sarcini simple, precum și în situații similare și noi.
Dezvoltarea. dezvolte abilitățile de auto-control și de control reciproc, dezvoltarea gândirii logice, competentă și execuție atentă.
Educativ: educația de independență și cultură colectivistă de exprimare.
Echipament: 2 jumătate de coli și o coală de hârtie pentru copiere, fiecare elev papetărie, foaie de contabilitate pentru fiecare elev.
1. Organizarea lecției.
Înainte de introducerea definiției unui trapez este util să amintim definiția unui paralelogram și să ia în considerare acest tip de patrulater, ale cărui numai două laturi opuse sunt paralele. (Determinarea trapezului este însoțită de un model de pe bord).
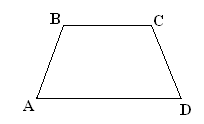
2. Asigurarea conceptului trapezului este gata prin desene de pe bord și problemele lor:
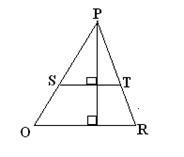
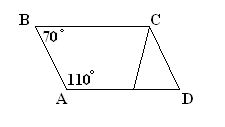
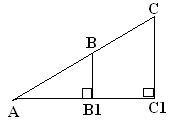
1) Care dreptunghiuri din Fig. a), b), c) este un trapez?
Sunați-le bază și părțile laterale.
Trapezul MNRK segment a avut loc PE // MN. Se determină tipul de MNRE patrulater.
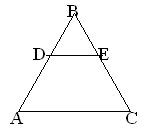
Într-un triunghi echilateral ABC cu laturile de 8 cm a avut loc linia de mijloc DE. Se determină tipul de ADES patrulatere. Care sunt laturile patrulaterului?
Luați în considerare elementele și numesc trapez, specii trapez.
3. Examinarea dovada linia mediană a trapezului.
După prezentarea dovezii este util să se stabilească etapele:
Construcție: segment de BE;
RO - linia de mijloc dublare.
Concluzie: PO // AD, PO = 1/2 (AD + BC)
Notă: (EP - linia de mijloc a trapezului, PO segment - poate fi văzută ca dublarea liniei mediane)
4. Consolidarea inițială a teoremei liniei mediane trece printr-o soluție de tipul de probleme:
1) Bazele trapezului 7 și 9 cm. Care este linia de mijloc a trapezului?
MN - linia de mijloc trapez ABCD. . După N t a avut loc o linie paralelă cu partea AB și partea AD se intersectează în punctul P. Dovedeste ca MNRA - paralelogram.
3) Într-un trapez ABCD secundar cunoscut: AB = 4 cm, BC = 6 cm, CD = 5 cm, AD = 10 cm Care sunt laturile trapezului AEFD dacă EF - linia mediană a trapezului.?
Fiecare dintre laturile ABCD trapezoid este împărțit în patru părți egale. Care sunt segmentele M N. M N și M N, în cazul în care AD = 11 cm, BC = 3 cm?
5) Republica Moldova - linia de mijloc a ABCD trapez cu bazele AD și BC = a = c. Traversează AC Diagonală C. Care sunt lungimile Republicii Kazahstan și Cabinetul?
6. Linia de mijloc a trapezului este egală cu 8 cm, iar unul dintre motive este de 6 cm. Care este altă bază?
Securizarea material nou prin sarcina propusă, se arată - așa cum este înțeles și am învățat materiale noi.
5. Rezumând lecția:
- denumirea elementelor sale;
- formularea teoremei despre midline.
Declarația de teme :. § 59 p 92-93, 17-19 întrebări, fund. №59 p.100.
Controlul asimilarea materialului se realizează prin testare (presupunând un control diferențiat al cunoștințelor studenților).
obligatorii Atribuirile parte discount pentru implementarea cu succes pe care elevii trebuie să utilizeze nivelul minim de cunoștințe în cerințele de software. parte suplimentară conține două sarcini nivelul mediu de complexitate, care corespunde cele mai multe dintre sarcinile majore ale manualului, și două sarcini pentru mai mulți studenți avansați.
Timpul necesar pentru testare se determină pe baza capacităților de o anumită clasă.
1) (1) Completați spațiile libere pentru a obține declarația din dreapta.
Linia de mijloc paralelă cu bazele trapezului și _____________
2) (1) În cazul în care MN - linia de mijloc trapez ABCD, atunci lungimea este egală cu MN ________________________________________________
AD si BC - baza trapez.
3) (2) Setați adevărate sau false următoarele afirmații:
A) Segmentul liniei care leagă laturile trapezului, se numește liniei centrale sale ________________
B) Dacă baza trapezului sunt 4 cm și 8 cm, linia de mijloc este de 4 cm ___________________
a) 7 cm; b) 5 cm; c) 3 cm.
5) (3) Într-una din bazele trapez mai lungi de încă 2 ori. Linia de mijloc a trapez = 15 cm. Găsiți baza sa.
a) 5 cm; 10 cm; b) 10 cm; 20 cm; c) 15 cm; 30 cm.
6) (3) Baza mică a trapezului se referă la linia medie de 2: 3. Obține lungimea de bază mai mică în cazul în care baza mai mare egală cu 16 cm.
a) 8 cm; 12 cm; b) 10 cm; 15 cm; c) 4 cm și 6 cm.
(4) Având în vedere: ABCD - trapez. AM = BM, BN = ND. Demonstrati ca MP - linia de mijloc a ABCD trapez.
8) (4) de 2 cm trapezoid mediană mai mică decât baza mai mare. Găsiți linia centrală a trapezului, în cazul în care baza este mai mică de 6 cm.
a) 8 cm; b) 10 cm; c) 5 cm.
9) (5) a unui trapez isoscel ABCD perpendicular a scăzut de la V vertex pe baza mai mare BD, se divide într-un interval egal cu 4 și 7 cm. Găsiți linia medie și baza mică a trapezului.
a) 10 cm; b) 4 cm; c) 8 cm.
10) (5) a unui trapez isoscel ABCD MN - linia de mijloc, BC = 6 cm, 14 cm MN = Calculați lungimea segmentului care este parte a liniei mediane și între diagonalelor minciuni trapez ..
a) 10 cm; b) 4 cm; c) 8 cm.