Vasilisa yaviks - motor de căutare inteligentă

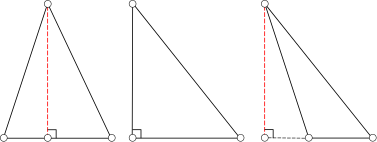
Înălțimea de triunghiuri de diferite tipuri

Înălțimea triunghiului - perpendiculara. a scăzut din vârful triunghiului în partea opusă (mai precis, pe linia care conține partea opusă). În funcție de înălțimea de tip triunghi poate fi conținut în interiorul triunghiului (triunghiul înclinat acut) coincide cu latura sa (care este piciorul unui triunghi dreptunghic), sau locul în afara triunghiului la triunghiul în unghi obtuz.

Proprietățile punctelor de intersecție ale celor trei altitudini ale triunghiului (The orthocenter)

• Toate cele trei înălțimi ale unui triunghi se intersectează într-un punct numit orthocenter. Această afirmație este ușor de dovedit prin utilizarea identității vector, care este valabil și pentru orice puncte. Nici măcar nu se află în același plan:

# X2192; # x22C5; # x2192; # x2192; # x22C5; # x2192; # x2192; # x22C5; # x2192;

(Pentru dovada identității trebuie să utilizeze formule

Ca un punct de intersecție E ar trebui să ia două înălțimi triunghi.)

• Ultima afirmație este, de asemenea, o consecință a teoremelor pe triunghiul pedalei topuri (înainte și înapoi)

• Orthocenter centrul isogonally conjugat al cercului circumscris.
• Orthocenter se află pe aceeași linie cu centrul de greutate. centrul cercului circumscris și un centru de cerc de nouă puncte (a se vedea. linia Euler).
• Orthocenter unui triunghi acută este centrul unui cerc înscris în ortotreugolnik lui.
• Centrul cercului descris despre un triunghi este orthocenter de triunghi cu vârfuri la punctele mediane ale laturilor triunghiului. Ultimul triunghi este numit un triunghi adăugat la primul triunghi.
• Această din urmă proprietate poate afirma ca: Cercul centru descris despre un triunghi este orthocenter triunghiului în continuare.
• Punctul orthocenter triunghi simetric față de laturile sale se află pe circumscris.
• Punctul simetric în raport cu orthocenter de triunghiul punctelor mediane laterale, de asemenea, bazate pe cercul circumscris și coincid cu punctele diametral opuse vârfuri corespunzătoare.
• Dacă O - centrul cercului descris ΔABC, # X2192; # x2192; # x2192; # x2192; .
  • # X2212; . în care: - raza cercului; - lungimea laturilor triunghiului.
• Distanța de la orthocenter de vertex triunghi de două ori distanța de la centrul cercului circumscris în partea opusă.
• Orice segment extras din orthocenter până la intersecția cu cercul circumscris este întotdeauna un multiplu al cercului Euler în jumătate. Orthocenter este centrul homothety al acestor două cercuri.
• Hamilton teorema. Trei segmente de linie care leagă orthocenter unui triunghi ascuțit cu vârfuri se împarte în trei triunghiuri cu același cerc Euler (cerc de nouă puncte), triunghiul acut original.
• Investigarea Hamilton teorema.
  • Trei segmente de linie care leagă nodurile cu orthocenter unui triunghi acut, se împarte în trei triunghi Hamilton. având raze egale de cercuri descrise.
  • Razele cercurilor de Hamilton trei triunghiuri sunt egale cu raza cercului circumscris despre triunghiul acut inițial.
  
  
  
  
  
  
  
• In triunghi unghi-acut, orthocenter se află în interiorul triunghiului; într-un obtuz - este un triunghi; într-un drept - la partea de sus a unghiului drept.

Proprietățile unui triunghi isoscel înălțimi

• În cazul în care cele două sunt egale cu înălțimea triunghiului, triunghiul - isoscel (teorema lui Steiner - Lemus), iar al treilea este înălțimea atât mediana și bisectoarea unghiului din care provine.
• Pe de altă parte, două înălțimi sunt egale în cadrul unui triunghi echilateral, iar al treilea este înălțimea atât mediana și bisectoarea.
• Într-un triunghi echilateral toate cele trei înălțimi sunt egale.

Proprietățile de bază ale înălțimilor triunghiului

• înălțimi baze formează o așa numită ortotreugolnik. Ea are propriile sale proprietăți.
• Ortotreugolnika descris despre cerc - un cerc al Euler. Pe acest cerc, de asemenea, pe trei laturi ale triunghiului si mijlocul celor trei segmente de mijloc trei se alătură orthocenter din vârfurile triunghiului.
• O altă formulare a celor mai recente caracteristici:
  • Teorema lui Euler pentru o nouă puncte cerc. Baze trei înălțimi triunghi arbitrar, trei din laturile sale de mijloc (baze medianele sale interne) și trei segmente de mijloc care leagă nodurile cu orthocenter. toate se află pe aceeași circumferință (pe o circumferință de nouă puncte).
• Teorema. In orice triunghi, segmentul care leagă baza celor două altitudini ale unui triunghi, triunghiul taie așa.
• Teorema. În segmentul de triunghi care leagă două înălțimi de triunghi de bază care se află pe ambele părți, o a treia parte antiparalel cu care nu are puncte comune. Doi dintre capătul său, precum și prin intermediul a două noduri ale respectivului terț este întotdeauna posibil pentru a desena un cerc.

Alte proprietăți ale înălțimilor triunghiului

• Dacă triunghiul este versatil (scalen), bisectoare sale interne. Prestate de la orice nod se află între interior și mediana realizat de aceeași înălțime la vârf.
• Triangle Inaltime isogonally Diametru conjugat (raza) al cercului circumscris. trase din același Vertex.
• Într-un triunghi-acută, înălțime două triunghiuri similare sale tăiat de la el.
• La înălțimea unui triunghi dreptunghic. trase din vârful unghiului drept. împarte în două triunghiuri similare cu originalul.

Proprietăți înălțimea minimă a triunghiului

Înălțimea minimă a triunghiului are multe proprietati extreme. De exemplu:

• proiecție ortogonală minimă a unui triunghi pe liniile situate în planul triunghiului are o lungime egală cu cea mai mică dintre înălțimea sa.
• secțiune dreaptă minimă într-un plan prin care puteți trage placa triunghiulară inflexibilă trebuie să aibă o lungime egală cu cea mai mică dintre înălțimile plăcii.
• Într-o mișcare continuă a două puncte de pe perimetrul triunghiului unul față de celălalt, distanța maximă dintre ele în timpul mișcării de la prima la a doua reuniune nu poate fi mai mică decât lungimea celor mai mici înălțimi triunghi.
• Înălțimea minimă a unui triunghi trece întotdeauna prin interiorul triunghiului.

relațiile de bază

• # X22C5; # x2061; # x03B3; # x22C5; # x2061; # x03B2;
• # X22C5; în cazul în care - zona triunghiului - laturile lungimea triunghiului, a cărui înălțime este omisă.
• # X2212; # x2212;
• # X22C5; # x22C5; unde # X22C5; - produsul laturilor, # X2212; raza circumscris
• # X22C5; # x22C5; # x22C5;
• . în care - raza cercului inscris.
• # X22C5; # x2212; # x22C5; # x2212; # x22C5; # x2212; . în cazul în care - zona triunghiului.
• # X22C5; # x22C5; # x2212; # x22C5; # x2212; # x22C5; # x2212; . - latură a triunghiului la care coboară înălțimea.
• Înălțimea triunghiului isoscel. a redus la baza: # X22C5; # x2212;

unde - baza - partea laterală.

• # X22C5; - înălțimea unui triunghi echilateral cu latura.

Teorema despre înălțimea unui triunghi dreptunghic

În cazul în care înălțimea unui triunghi dreptunghiular lungime ABC. Prestate de la vârful unghiului drept împarte lungimea ipotenuzei și pe segmentele. Catete și adecvate. atunci egalitățile sunt adevărate:

O teoremă pe proiecții

A se vedea. Pentru a. 51, p. (1.11-4). O teoremă pe proiecții: # X2061; # x03B2; # x2061; # x03B1; # x2061; # x03B3; # x2061; # x03B2; # x2061; # x03B1; # x2061; # x03B3; . Din teorema privind proiecțiile ar trebui să fie faptul că înălțimea, a redus, de exemplu, din partea de sus. divide partea opusă în două părți # X2061; # x03B2; și # X2061; # x03B1; . măsurată de la vârf până la.

poem mnemonic

Înălțimea este ca o pisica,
Ceea ce, arcuiesc spatele lui,
Și la un unghi drept
conectați sus
Și spre coada.

Variațiuni pe tema. Înălțimea patrulaterul

Teorema. Să - inscripționată patrulater, - suprafata normala (ridicat), a redus din partea superioară a diagonalei; în mod similar, determinat de puncte. Apoi, punctele se află pe un cerc.

notițe