Numărul de module
Pentru prima dată, cu numărul modulului, ne-am întâlnit în clasa a șasea, în cazul în care o astfel de definiție dată: numărul modulului este distanța (în intervalul unitate) de la origine la punctul. Această definiție dezvăluie semnificația geometrică a modulului.
Modulul unui număr real - este valoarea absolută a acestui număr.
Pur și simplu pune, modulul de captare a fi scăzut de la numărul de semnul său.
a unui modul notat | A |. Notă: numărul modulului este întotdeauna nenegativ: | o | ≥ 0.
| 6 | = 6, | -3 | = 3, | -10,45 | = 10.45
Modul de definire
proprietăţile modulului
1. Numerele opuse Module sunt egale
2. Pătratul modulului este egală cu pătratul acelui număr,
3. rădăcina pătrată a pătratului numărul unui modul al acestui număr
4. Numărul modulului este numărul de non-negativ
5. factor constant pozitiv poate fi luată în afara mărcii modulului
7. Produs Modul de două (sau mai multe) a numerelor este egală cu produsul dintre moduli
Sensul geometric al modulului
Numărul modulului - distanța de la zero la un anumit număr.
Luați în considerare cea mai simplă ecuație | x | = 3. Se poate vedea că pe linia numărul, există două puncte a căror distanță de la zero este egal cu trei. Aceasta punctele 3 și -3. Deci, ecuația | x | = 3, există două soluții: x = 3 și x = -3.
Această ecuație poate fi citit ca distanța de la punctul de la punctul de ingrijire. Cu ajutorul metodei grafice poate determina că ecuația are două soluții :.
Noi rezolva inegalitatea: | x + 7 | <4 .
Acesta poate fi citit ca: distanța de la un punct la mai puțin de patru. A: (-11, -3).
Noi rezolva inegalitatea: | 10 - x | ≥ 7.
Distanța de la punctul 10 la punct mai mare sau egal cu șapte. Răspuns: (-∞; 3] υ [17, + ∞)
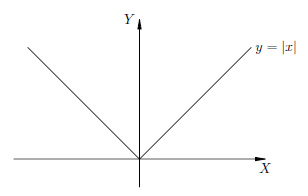
Graful y = | x |
Pentru x≥ 0 avem y = x. pentru x <0 имеем y = -x.
Rezolvarea ecuații și inegalități conținând numărul modulului
La soluționarea problemelor, conținutul unei unități de număr real, metoda de bază este dezvăluirea unei plăci modulului în funcție de proprietățile sale.
Astfel, în cazul în care există o expresie a semnului modulului, în funcție de variabila, deschidem definitia modulului:
În unele cazuri, modulul este dezvăluită în mod clar. De exemplu: ca expresie a semnului modulului este non-negativ, la toate
